Определение операций для сокращения времени их выполнения.

Наиболее сложной задачей при построении графика стоимости времени является нахождение прямых издержек для конкретных продолжительностей npoei ia Особую озабоченность вызывает вопрос: продолжительность каких операций сокращать и до какой степени? В сущности, менеджеры должны рассматривать критические операции, время выполнения которых можно сократить с наименьшим повышением стоимости на единицу времени. Обоснование выбора критических операций зависит от определения стандартного и предельного времени выполнения операции и соответствующих затрат. Обычное время выполнения операции означает низкую стоимость, реалистичность, эффективные методы для выполнения операции в нормальных условиях. Сокращение времени выполнения операции называется авралом (crashing). Кратчайшее время, за которое операция реально может быть выполнена, называется ее предельным временем (crash time). Прямые затраты на выполнение операции в ее предельные сроки называются стоимостью срочной операции. Информацию об обычном и предельном времени получают от персонала, знакомого с выполнением операции. На рис. 6-2 изображен график стоимости времени выполнения гипотетической операции. Обычное время выполнения операции — 10 единиц и соответствующая стоимость — $ 400, Предельное время выполнения операции — 5 единиц и стоимость — $ 800. Пересечение обычного времени и стоимости представляет начальную низкую стоимость и раннее начало выполнения графика. Жирная линия, соединяющая точки обычного и предельного времени, представляет наклонную, что предполагает, что затраты на сокращение времени операции постоянны в единицу времени. Предположения, лежащие в основе использования этого графика, следующие:.

1.

Отношения стоимости ко времени — линейные.

2.

Обычное время предполагает низкую стоимость, эффективные методы для завершения операции.

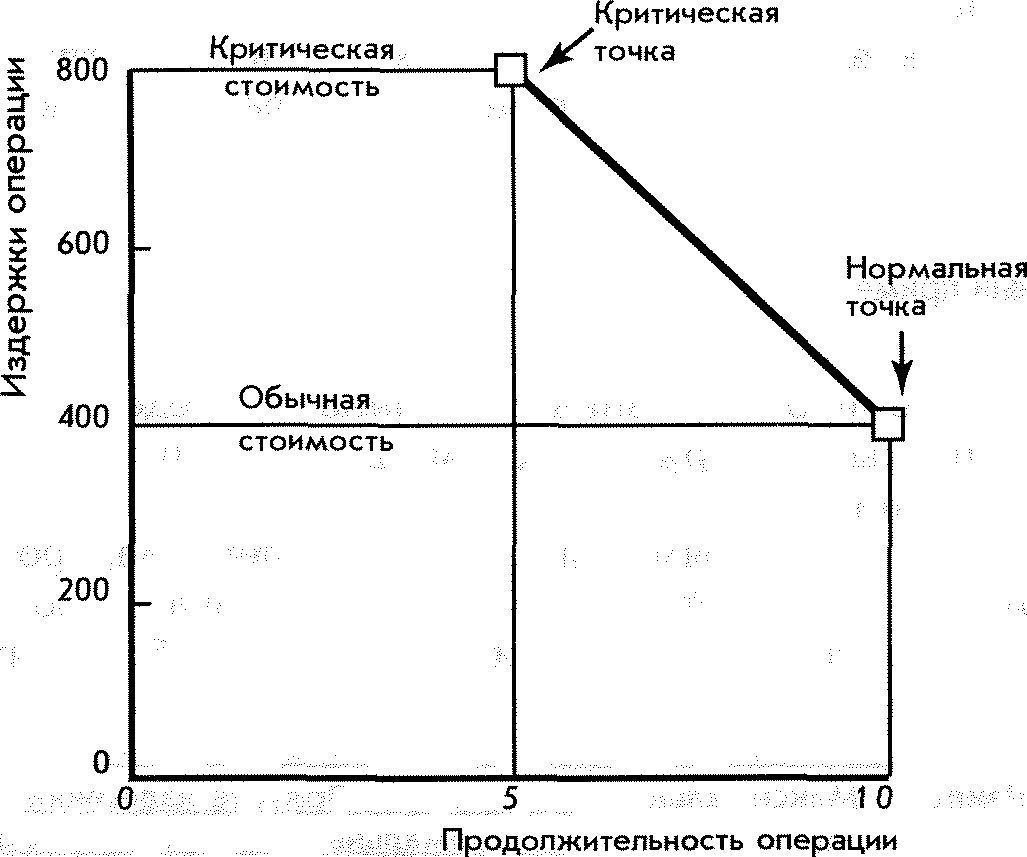
Рис. 6-2. График стоимости времени выполнения опервции.

3.

Предельное время представляет лимит — наиболее возможное сокращение времени в реальных условиях.

4.

Наклонная линия представляет затраты в единицу времени.

5.

Все ускорения должны происходить в рамках обычниго и предельного времени.

Знание наклона операций позволяет менеджерам сравнить и выбрать критические операции, время выполнения которых можно сократить. Чем меньше угол наклона операции, тем меньше издержки на сокращение периода времени; более крутая наклонная означает, что потребуется больше средств на сокращение одной единицы времени. Стоимость одной единицы времени или наклонной для любой операции рассчитывается по следующему уравнению:

На рис. 6-2 таким подъемом является ось Y (стоимость), а периодом — ось X (продолжительность). Наклонная стоимости — $ 80 каждой единицы времени, на которые сокращена операция; предельное сокращение времени операции — 5 единиц. Сравнение наклонных всех критических операций позволяет нам определить, какие операции нужно сокращать, чтобы минимизировать общие прямые издержки. Имея предварительный график проекта (или тот, который уже в работе), со всеми операциями и их.

ранним временем начала, можно приступить к процессу поиска критических операций, время выполнения которых можно сократить. Необходимо найти общую сумму прямых издержек для сокращения каждой конкретной продолжительности проекта.

Упрощенный пример.

На рис. 6-3а представлены обычное и предельное время и издержки для каждой операции, рассчитанная наклонная и предел сокращения времени, общие прямые издержки и схема проекта продолжительностью в 25 единиц времени.

Отметим, что общие прямые издержки для периода, продолжительностью в 25 единиц — $450. Это важная точка для начала процедуры сокращения времени критического пути и нахождения общих прямых издер-

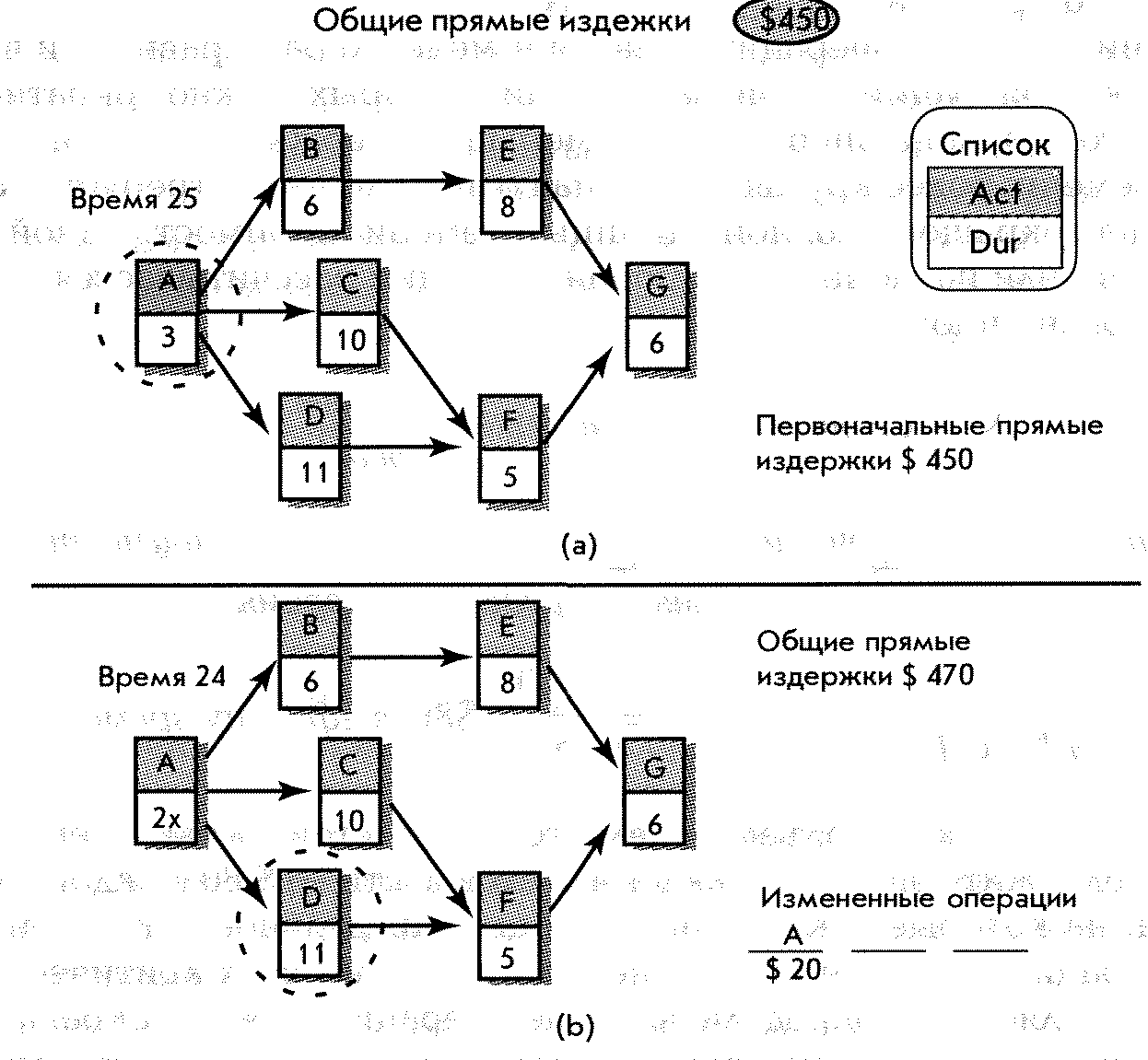
жек для каждой конкретной операции продолжительностью меньше чем 25 единиц. Максимальное время, на которое операция может быть сокращена, представляет разницу между обычным и предельным временем выполнения операции. Например, операция D может быть сокращена с обычной продолжительности в 11 единиц времени до предельного времени в 7 единиц, или максимально на 4 единицы времени. Положительная наклонная для операции D рассчитывается следующим образом:.

Стоимость срочной программы-Обычная стоимость

Наклон=-—-——г-=.

Обычное время-Предельное время.

$150—$50 $100.

На схеме видно, что критический путь представлен операциями A,D,F,G. Так как невозможно сократить операцию G, операция А обведена кружком, поскольку является наименее дорогой; то есть ее наклонная ( $20) меньше, чем наклонные операций D и F($ 25 и $ 30). Сокращение операции А на одну единицу времени сокращает продолжительность проекта до 24 единиц времени, но увеличивает общие прямые издержки до $ 470 ($ 450 + $ 20 = $ 470). Рис. 6-3в отражает эти изменения. Продолжительность операции А сократилась до двух единиц времени; «х» показывает, что операция не может больше сокращаться. Операция D обведена потому, что она наименее дорогая ($ 25), чтобы сократить время проекта до 23 единиц времени. Сравните стоимость операции F. Общие прямые издержки проекта продолжительностью в 23 единицы времени составят $ 495 (см. рис. 6-4а).

Обратите внимание, что схема проекта на рис. 6-4а теперь имеет два критических пути—A,C,F,G и A,D,F,G. Сокращение продолжительности проекта до 22 единиц времени потребует сокращения продолжительности операции F, поэтому она обведена. Эти изменения показаны на рис. 6-4в. Общие прямые издержки для продолжительности в 22 единицы времени составят $ 525 . Это сокращение приведет к возникновению третьего критического пути — A,B,E,G; все операции критические. Наименее дорогостоящим методом сокращения продолжительнос ти проекта до 21 единицы времени является комбинация обведенных операций C,D,E, стоимость которых соответственно $ 30, $ 25, $ 30, и увеличение общих прямых издержек до $ 610.

Результаты этих изменений отражены на рис. 6-4с. Хотя некоторые операции все еще можно сократить (те, которые не имеют «х» у времени операции), ни одна операция или их комбинация не приведут к сокращению продолжительности проекта.

Имея общие прямые издержки для множества конкретных продолжительностей выполнения проекта, следующий шаг, который нужно сделать, — это собрать косвенные издержки для различных продолжительностей. Эти издержки обычно представляют ежедневную ставку и их легк© получить в бухгалтерии. В табл. 6-1 представлены общие прямые издержки, общие косвенные издержки и общие издержки проекта.

Те же издержки внесены в рис, 6-5. На этом графике показано, что оптимальная стоимость продолжительности в 22 единицы времени — $ 775.

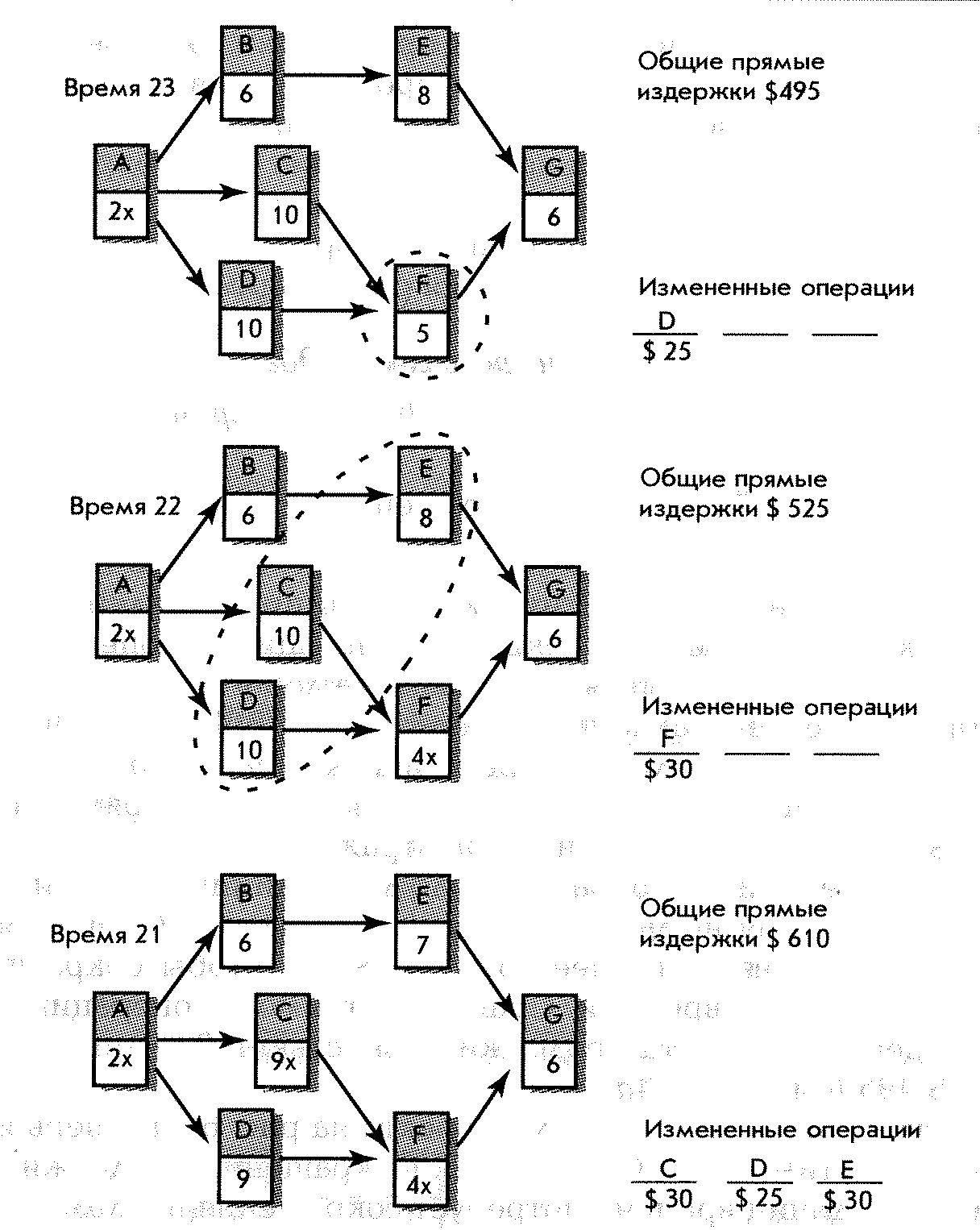
Таблица 6-1. СУММА ИЗДЕРЖЕК ПО ПРОДОЛЖИТЕЛЬНОСТИ

Предположим, что проект будет реализован, как планировалось, тогда любое отклонение от времени продолжительности увеличит издержки проекта. Отклонение от 25 до 22 происходит потому, что в этом диапазоне угол наклона косвенных издержек больше, чем угол наклона прямых издержек.