Проекты, ограниченные по времени.

При составлении календарного плана ограниченного по времени проекта внимание сосредоточено на использовании ресурсов. Если потребность в конкретном типе ресурсов колеблется, то управление затрудняется, и использование может быть весьма неэффективным. Практики решают эту проблему, используя метод выравнивания ресурсов, который уравнивает или сглаживает потребность в ресурсах. В сущности, все методы выравнивания приводят к задерживанию некритических операций, используя простои для снижения пика потребностей и восполняя их нехватку. Это можно продемонстрировать на гипотетическом примере.

При демонстрации этого примера будет использован только один тип ресурсов (например, плотники); в рамках этого типа все ресурсы взаимозаменяемы.

Начальной точкой для выравнивания ресурсов является ранний старт (ES) сетевого плана. На рис. 7-2 представлен пример сети, ES графика потребности в ресурсах и график использования ресурсов. Затемненные области на графике потребности представляют границы календарного графика для каждой операции. Обратите внимание на колебания потребности в ресурсах, отраженные на графике использования ресурсов. Поскольку было заявлено, что проект ограничен по времени, целью будет сокращение пика потребностей в ресурсах и, таким образом, повышение степени их использования. Изучение ES графика загрузки ресурса показывает, что только две операции имеют простой, который можно использовать для сокращения пика — операции В и D, Любая из этих операций может быть задержана, чтобы сократить пик потребности в ресурсах от 5 до 4, используя 2 единицы времени простоя. Выбор, очевидно, будет сделан в пользу операции, которая имеет наименьший риск опоздания (вероятно, операция D, поскольку она имеет наибольший простой). На рис.7-ЗА показаны результаты задержки операции В. На рис, 7-ЗВ показаны результаты задержки операции D. Обратите внимание на различие в графиках ресурсов. Важным моментом является то, что ресурсы, необходимые на время существования проекта, были сокращены с 5 до 4 (20%) и использование ресурсов возросло с 57% [необходимые 34 единицы ресурсов в целом (5x12)] до 71% [34/(4x12)]. Кроме того, график был выровнен, что означает облегчение в управлении.

Обратной стороной процесса выравнивания потребности в ресурсах является потеря эластичности сетевого графика, которая происходит в результате сокращения резервов времени выполнения работ. Риск того, что какие-то операции могут задержать проект, также увеличивается, поскольку сокращение резервов времени выполнения работ приводит к появлению большего числа критических и/или почти критических операций. Стремление слишком сильно выровнять график ресурсов рискованно. Тогда каждая операция становится критической.

Этот простой пример помогает понять проблему ограничения по времени и метод выравнивания. Однако на практике даже для небольших проектов проблема представляет значительную сложность. Неавтоматизированное решение проблемы не имеет смысла. К счастью, имеются пакеты программ, которые имеют хорошие способы выравнивания ресурсов проекта.

Обычно для выравнивания ресурсов проекта используются операции, которые имеют наибольший резерв времени их выполнения. Это объясняется тем, что с такими операциями связан наименьший риск. Хотя обычно это и верно, другие факторы риска, такие как уменьшение эластичности при перераспределении ресурсов для выполнения других операций или характер операции (простая, сложная), не берутся в расчет при использовании простых обоснований. Требуется, как правило, исследовать множество вариантов, прежде, чем найдется тот, который лучше всего подходит для проекта и сводит к минимуму риск запаздывания проекта в целом. Некоторые процедуры, используемые при выполнении компьютерных операций, можно встретить в классических работах.

Проекты, ограниченные по количеству ресурсов.

Когда количество людей и/или оборудования не соответствует удовлетворению пика потребностей и их невозможно получить в большем количестве, руководители проектов сталкиваются с проблемой ограниченных ресурсов. Что-то надо предпринимать. Искусство заключается в том, что неооходимо определить приоритеты и распределить ресурсы таким образом чтобы свести к минимуму задержку проекта, не превышая при этом лимит ресурсов и не изменяя технические отношения сети. Проблема составления календарного графика ресурсов представляет большую комби-

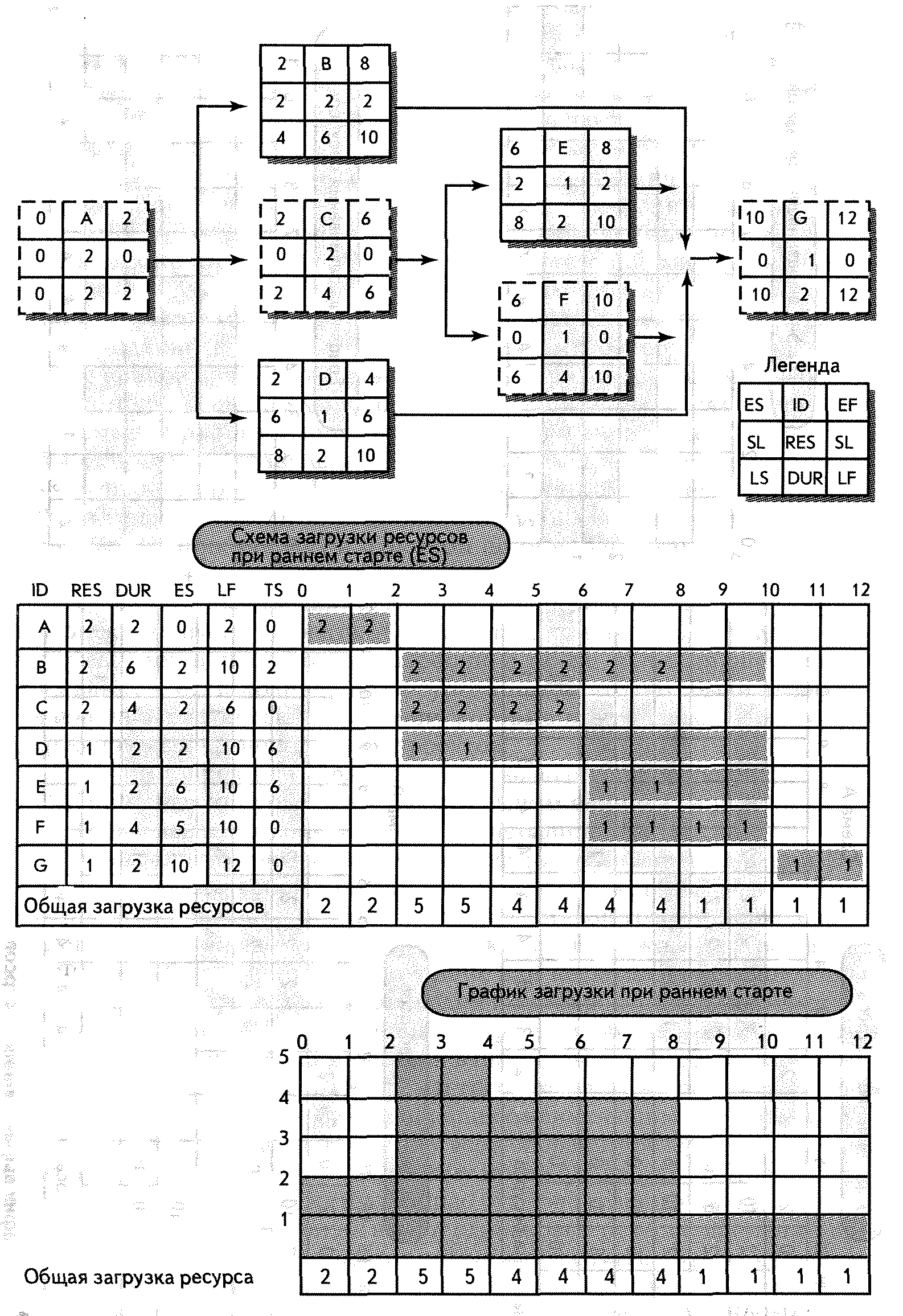
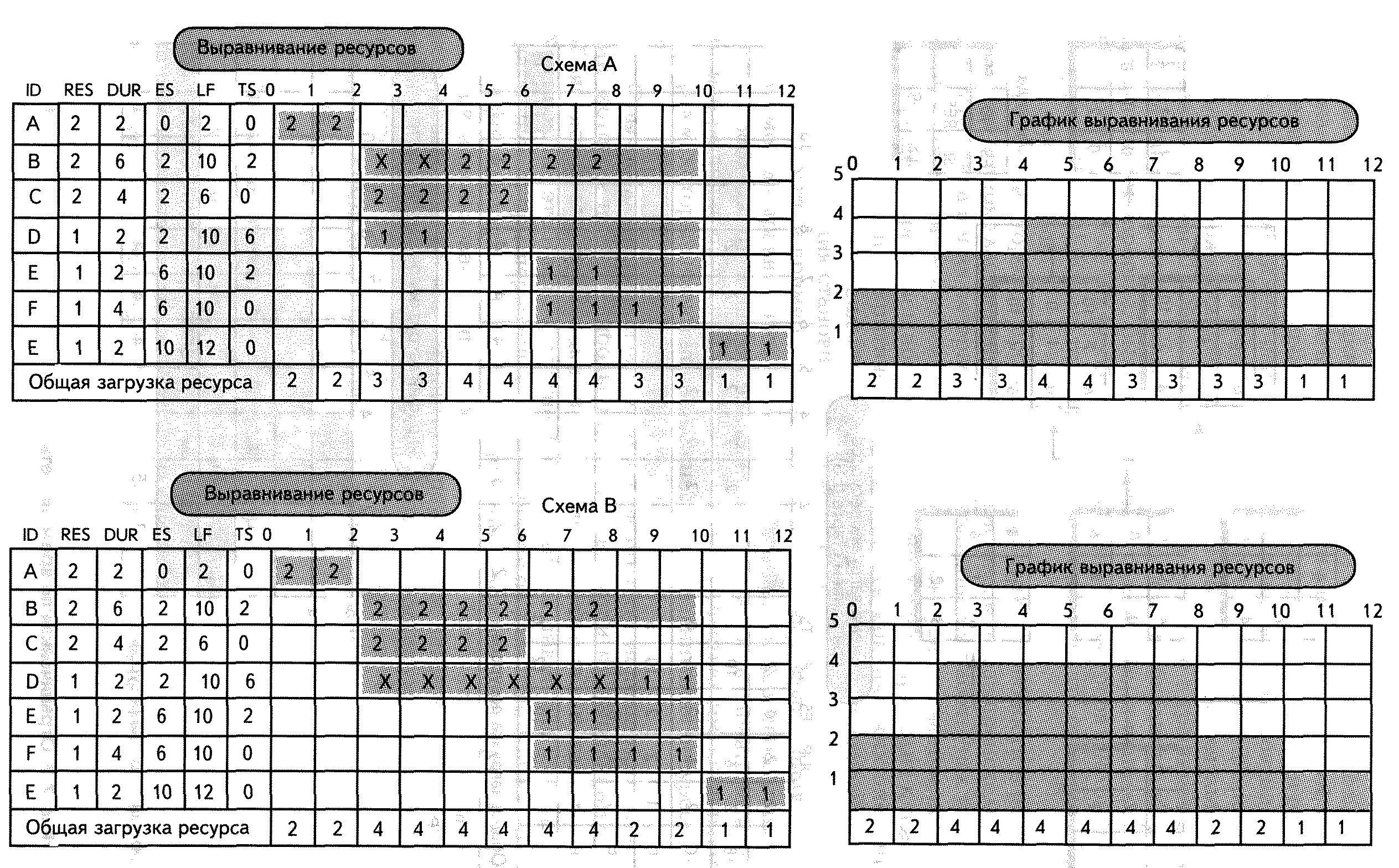
Рис. 7-3. График выравнивания ресурсов.

наторную проблему. Это значит, что сеть даже весьма небольшого проекта всего лишь с несколькими типами ресурсов может иметь несколько тысяч возможных решений. Несколько исследователей продемонстрировали оптимум математических решений проблемы распределения ресурсов для небольших по своим размерам сетевых графиков с весьма незначительным количеством типов ресурсов. Огромное количество данных, которое требуются для более крупных проблем, сделало практически нецелесообразными чисто математические решения (например, линейное программирование). Альтернативным подходом к проблеме было использование эвристического (приближенного метода) для решения больших комплексных проблем. Такие практические решения или правила приоритета долгое время применялись на практике. Эвристика не всегда дает оптимальный календарный график, но весьма подходит для составления «хороших» графиков для очень сложных сетей с разными типами ресурсов. Однако, поскольку каждый проект уникален, в его сетевом графике имеет смысл пробовать применить несколько эвристических наборов, чтобы определить правила приоритетного распределения с минимально и задержкой проекта. Имеющиеся сегодня компьютерные программы позволяют руководителю проекта создать для проекта хороший календарный график ресурсов. Простой пример эвристического подхода приводится ниже.

Ресурсы для выполнения операций распределены так, чтобы уменьшить риск отставания проекта от заданного срока; то есть, определен приоритет выделения ресурсов на операции, а также то, какие операции задерживаются, если количество ресурсов недостаточно. Были выявлены следующие эвристические критерии, которые всегда сводят к минимуму задержку самых разнообразных проектов:.

1.

Минимум резерва времени начала выполнения операции.

2.

Наименьшая продолжительность выполнения операции.

3.

Наименьший порядковый номер операции.

Наиболее часто применяется метод распараллеливания операций. Этот метод представляет собой итерационный процесс, который начинается в исходной точке проекта, и затем исследует сетевой график период за периодом с целью определения операций, которые должны начаться в данном периоде. Если для выполнения двух или нескольких установленных таким образом операций требуются одни и те же ресурсы, то применяется правило приоритетности выделения ресурсов (из числа названных выше или каких-то других). Например, если в пятом периоде должны начаться 3 операции (т.е. они имеют тог же ES ) и требуют таких же ресурсов, то первой операцией на графике будет операция с наименьшим резервом времени (применяем правило 1). Но если у всех операций резерв времени одинаков, нужно обратиться к следующему правилу (правило 2), тогда операция с наименьшей продолжительностью будет на графике первой. В очень редких случаях, когда операции имеют одинаковые резервы времени и продолжительности, связь нарушается операцией с самым низким идентификационным номером (правило 3), поскольку каждая операция имеет свой индивидуальный номер (ID). Когда лимит ресурсов достигнут, ранний старт (ES) последующих операций, которые еще не внесены в график, будет задержан (все последующие операции, не имеющие свободного резерва времени) и их резерв времени сократится. В последующие периоды процедура повторяется до тех пор, пока не будет составлен график всего проекта. Эту процедуру можно применить к упомянутым ранее примерам проекта (см. рис. 7-ЗА и В), только теперь фонд ресурсов ограничен тремя операциями. Рассмотрите, какие действия обозначены на рис, 7-4 и 7-5. Обратимся к рис. 7-4.

Заметьте, как важно корректировать каждый период, чтобы отражать изменения в самом начале резерва времени выполнения операции, чтобы действительность могла отражать изменения приоритетов.

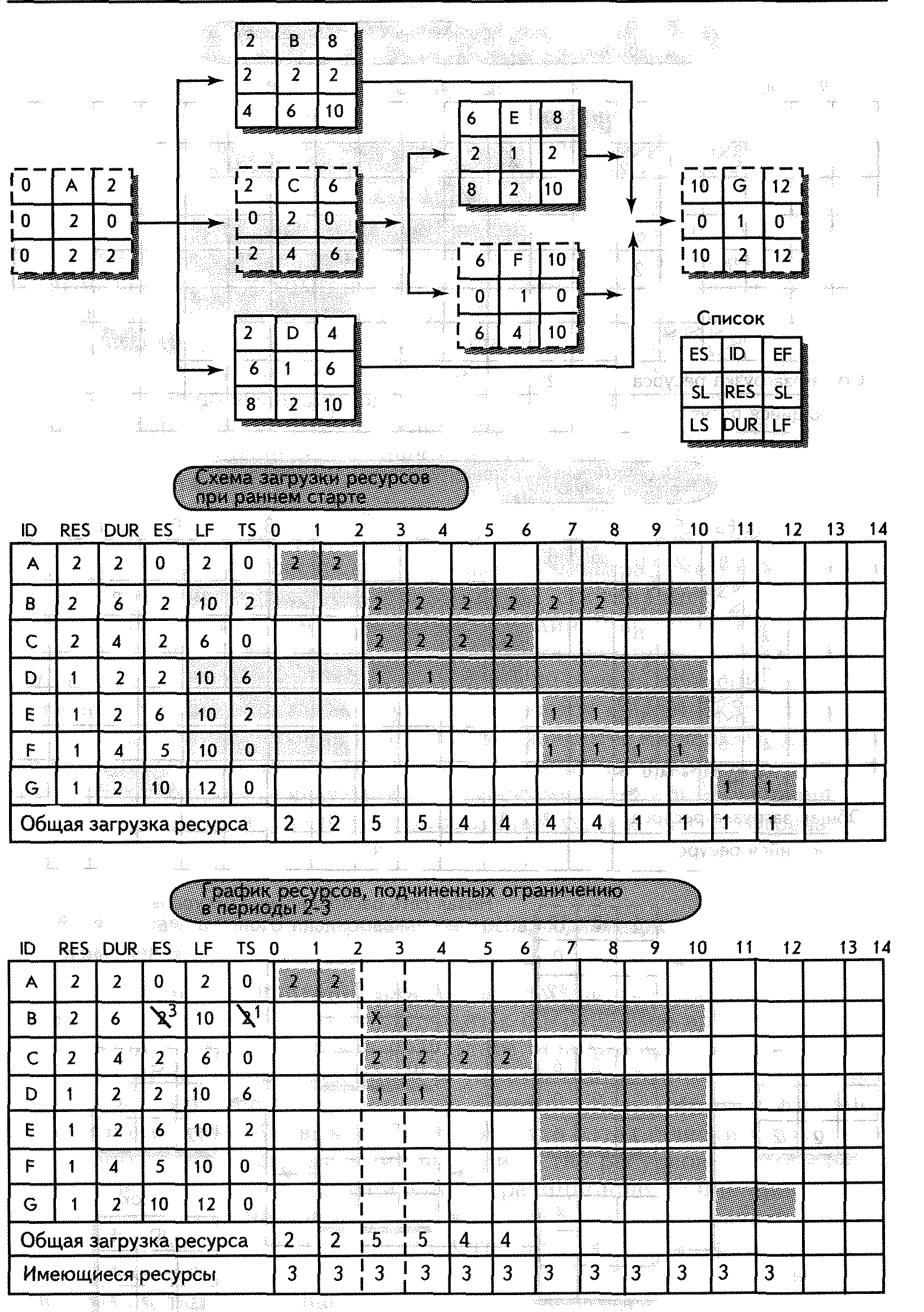
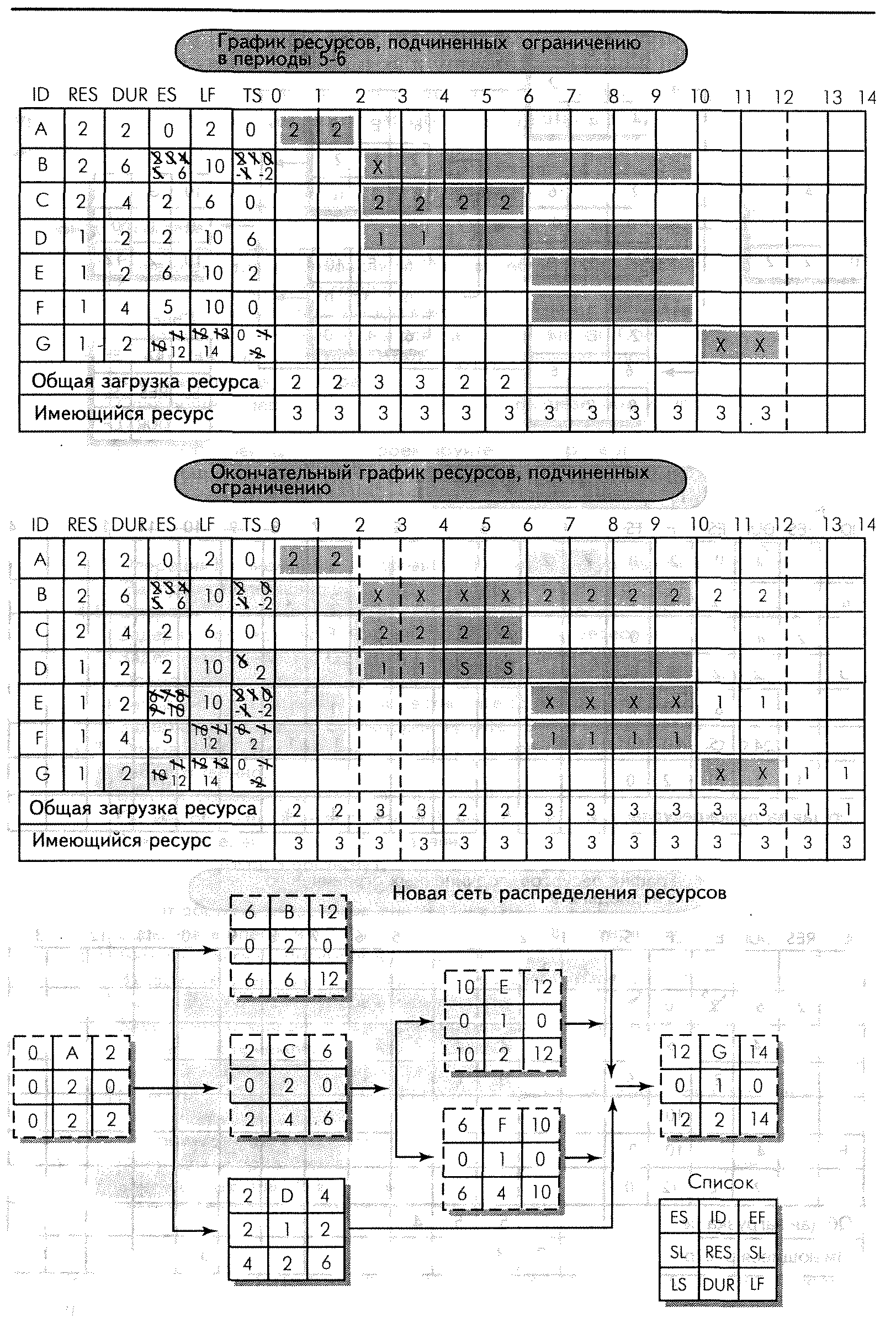
В сети на рис. 7-5 на графике календарного планирования указана новая дата в 14 единиц времени против продолжительности в 12 единиц времени проекта, подчиненного ограничениям по времени. Сеть была скорректирована и отражает новое время начала, окончания и резервы времени для каждой операции. Обратите внимание, что операция F все еще остается критической, и ее резерв — 0, потому что ресурсов в наличии нет (они используются в операциях В и Е). Сравните резервы времени для каждой операции на рис. 7-4 и 7-5; резервы времени значительно сократились. Заметьте, что операция D имеет только 2 единицы резерва времени, а не 6 единиц, как раньше. Это происходит потому, что имеются только 3 ресурса, которые необходимы для удовлетворения потребности в ресурсах операций В и Е. Кроме того, что продолжительность проекта увеличилась с 12 до 14 единиц времени, количество критических операций (А, В, С, Е, F, G) возросло с 4 до 6.

На рис. 7-6 показана другая сеть проекта, когда используются три различных типа ресурсов (А, В и С); общий фонд каждого типа состоит из 2 ресурсов. Первоначальный критический путь показан в сети пунктирной линией. А критические операции с использованием ограниченных ресурсов изображены в блоках операций, выделенных сплошными толстыми линиями. Ниже сетевого графика приводится график потребности в ресурсах. Время («план») и ресурсы показаны внизу на графике 7-6. Время, которое ограничивает критический путь, составляет 3, 5, 8 и 11, продолжительность проекта составляет 17 единиц времени. Ресурсы, которые ограничивают выполнение критических операций, составляют 1, 4,.

5, 7, 8 и 10 при продолжительности проекта 20 единиц времени. Обратите внимание, что операции 3 и 11 уже не являются критическими и имеют резервы времени. Операции 4, 5, 7 и 8 уже являются не параллельными, а последовательными. Резервы времени сократились. Ресурсы А, В, и С в какой-то точке проекта являются критическими. Хотя примеры на рис. 7-5 и 7-6 гипотетические, проиллюстрированные условия часто встречаются на практике.

Влияние календарного планирования ресурсов, подлежащих ограничениям.

Как и при выравнивании ресурсов, календарное планирование ограниченных ресурсов обычно приводит к сокращению времени простоев, снижению эластичности в результате использования времени простоев для минимизации задержек и увеличению количества критических и почти критических операций. Сложность календарного планирования увеличивается в результате того, что к техническим ограничениям прибавляются ограничения на количество ресурсов; время начала может иметь теперь два ограничения. Традиционная концепция последовательного выполнения операций критического пути с начала до конца проекта уже не имеет значения. Ограничения на ресурсы могут нарушить последовательность, и в сети могут оказаться несвязанные критические операции. И, наоборот, параллельные операции могут стать последовательными. Операции с резервами времени выполнения на сетевом графике могут перейти из разряда критических в разряд некритических, а некоторые критические операции могут стать некритическими с резервом времени.