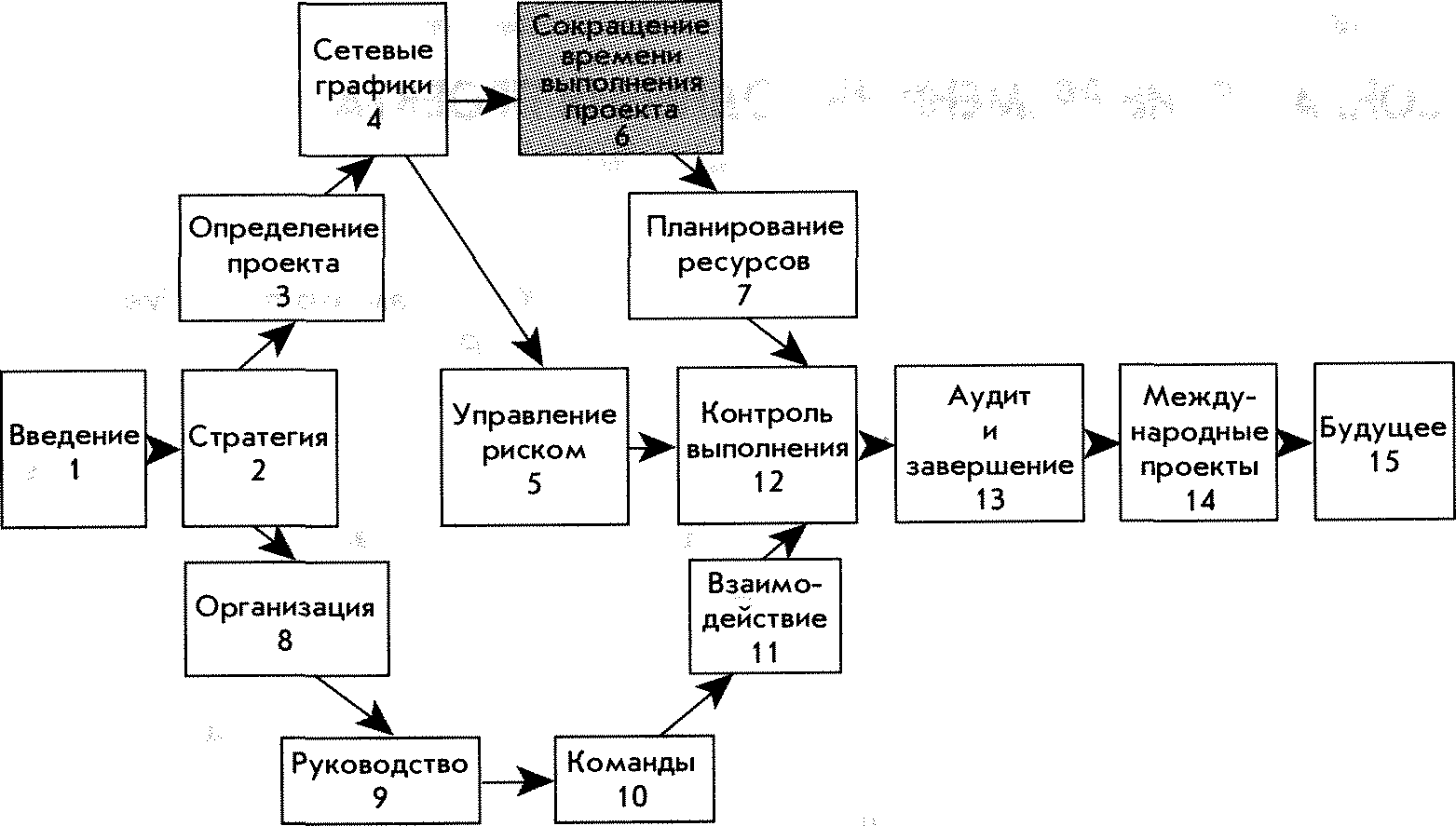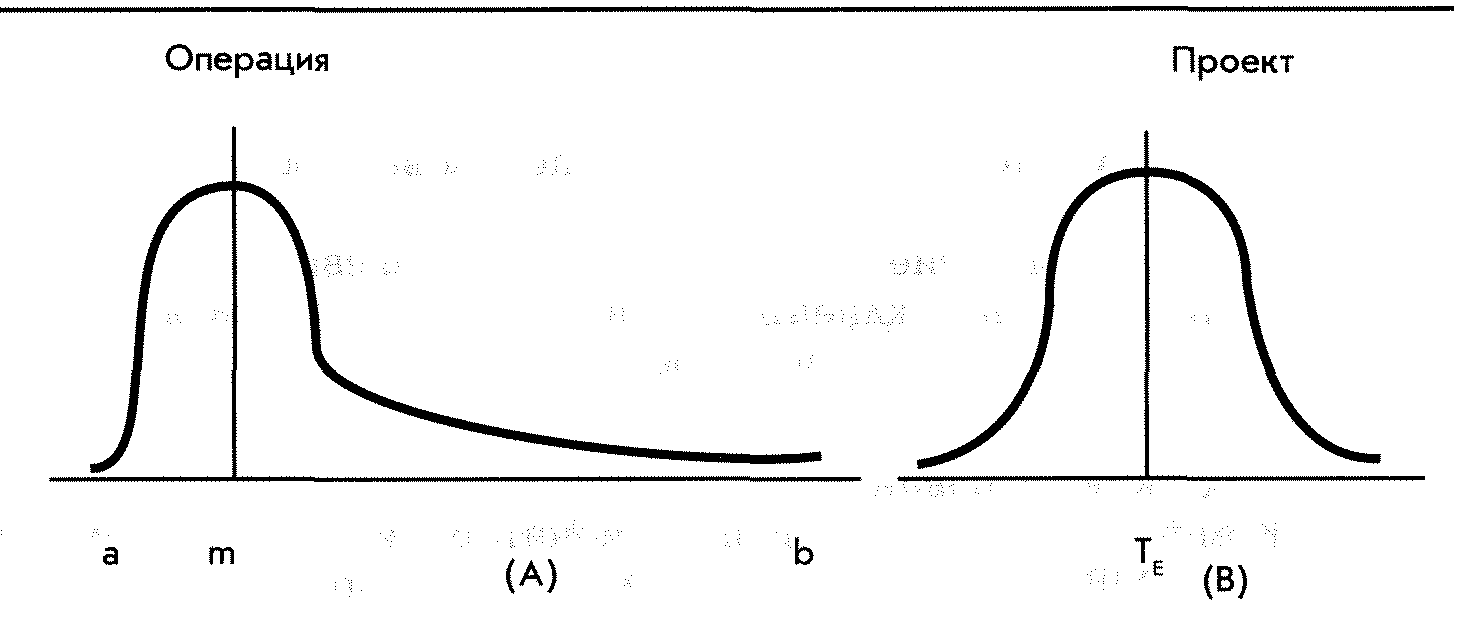
Рис. А 5-1. Операция и плотность распределения проекта.
будет продолжаться и дальше, то разработчики PERT для выражения продолжительности операции решили избрать аппроксимацию бета-распределения (бета-дистрибуции). Известно, что данное распределение (дистрибуция) является гибким и может содержать эмпирические данные, не следующие за нормальным распределением. Время операции может отклоняться либо больше в сторону верхнего, либо больше в сторону нижнего предела данных. На рис. А5-1(А) представлено бета-распределение (дистрибуция) для продолжительности операции, отклоняющееся вправо, и оно представляет собой работу, которая имеет тенденцию отставать от графика, раз уж так случилось вначале.
Распределение продолжительности проекта показано в симметрии на рис. А5- 1(B). Распределение проекта представляет собой сумму средневзвешенных показателей операций на критическом пути.
Знание средневзвешенного показателя и отклонения для каждой операции позволяет планирующему проект рассчитать вероятность различных продолжительностей проекта. Проследите этапы, описанные на приводимом ниже гипотетическом примере. (Терминология будет трудна для незнакомых со статистикой, но процесс покажется легким, если его повторить еще на нескольких примерах.).
Средневзвешенное время операции рассчитывается по следующей формуле:
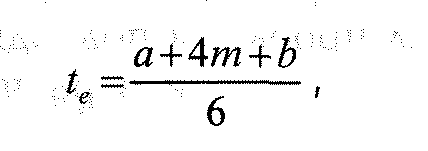
(5-1).
где t
— средневзвешенное время операции;.
а — оптимистическое время операции (1 шанс из 100, что при нормальных условиях операция будет закончена раньше срока); b — пессимистическое время операции (1 шанс из 100, что при нормальных условиях операция будет закончена позже срока); т —наиболее вероятное время операции.
После точного определения трех расчетов времени это уравнение используется для вычисления средневзвешенной продолжительности для каждой операции. Среднее (детерминистическое) значение накладывают на сеть проекта, как и при использовании СРМ, и затем рассчитывают раннее, позднее, резервное и время завершения проектных работ, как они указаны в СРМ.
Отклонения в оценках времени операции определяются при помощи следующих уравнений. Уравнение 5-2 представляет стандартное отклонение для операции. Уравнение 5-3 представляет стандартное отклонение для проекта. Обратите внимание на то, что стандартное отклонение для операции в этом уравнении возведено в квадрат; это называется дисперсия (среднее отклонение). Эта сумма включает в себя только виды операций на критическом или проверенном пути.
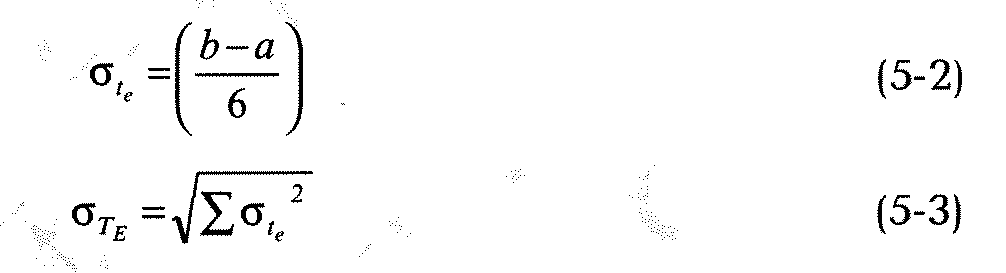
И, наконец, средняя продолжительность проекта (Т
) — это сумма всех средних показателей времени, отведенных на выполнение операций по критическому пути (сумма от te), и она следует нормальному распределению (дистрибуции).
Зная среднюю продолжительность проекта и дисперсии (среднего отклонения) операций, можно с помощью статистических таблиц рассчитать выполнение проекта (или сегмента проекта) к конкретному времени. Уравнение 5-4 используется для расчета величины Z, приводимой в статистических таблицах (Z — количество стандартных отклонений от средней величины), что в свою очередь показывает вероятность выполнения проекта в указанные сроки:

где Т
— продолжительность критического пути;.
T
— продолжительность работы по графику;.
Z — вероятность (выполнения графика), определенная по статистической таблице А5-2.
Гипотетический пример использования метода PERT.
Продолжительность операций и значение среднего отклонения представлены на таблице А5-1. Сеть проекта представлена на рис. А 5-2.
Прогнозируемый срок работы (Т
) представлен 64 единицами времени; критический путь— 1, 2, 3, 4, 5, 6. Имея эту информацию и используя стандартные статистические методы, можно легко рассчитать вероятность выполнения проекта к конкретному времени. Например, какова вероятность завершения работы над проектом до указанного в графике времени (T
) из 67? Обычная кривая проекта будет такой, как на рис. А 5-3.
Таблица А5-1. ВРЕМЯ/ДЛИТЕЛЬНОСТЬ ОПЕРАЦИЙ И ИХ РАЗЛИЧИЯ | |||||
Операция | а | Ь | t. е | [(Ь—а)/6] г | |
1—2 | 17 | 29 | 47 | 30 | 25 |
2—3 | 6 | 12 | 24 | 13 | 9 |
2—4 | 16 | 19 | 28 | 20 | 4 |
3—5 | 13 | 16 | 19 | 16 | 1 |
4—5 | 2 | 5 | 14 | 6 | 4 |
5—6 | 2 | 5 | 8 | 5 | 1 |
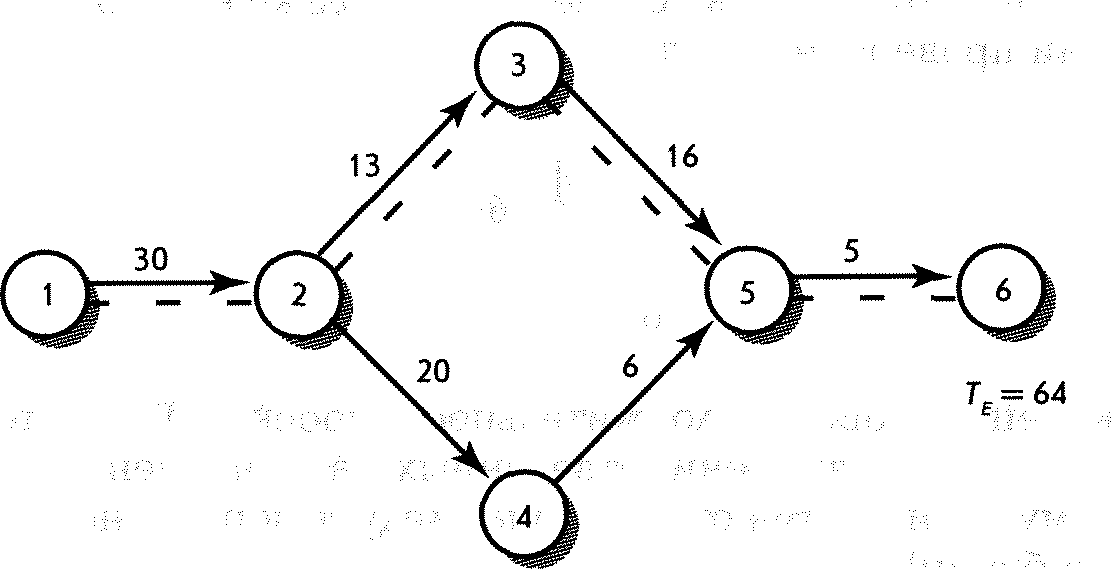
Рис. А5-2. Гипотетическая сеть
Таблица А5-2 | |||
Величина Z | Вероятность | Величина Z | Вероятность |
-2,0 | 0,02 | +2,0 | 0,98 |
-1,5 | 0,07 | +1,5 | 0,93 |
-1,0 | 0,16 | +1,0 | 0,84 |
-0,7 | 0,24 | +0,7 | 0,76 |
-0,5 | 0,31 | +0,5 | 0,69 |
-0,3 | 0,38 | +0,3 | 0,62 |
-0,1 | 0,36 | +0,1 | 0,54 |
^25+9+1+1 V36 Р» 0,26.
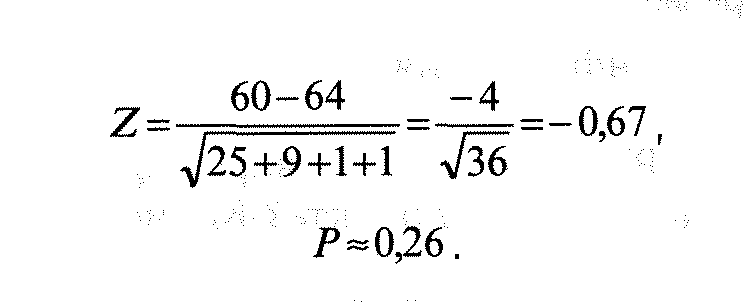
По таблице А 5-2 значение Z — 0,6? дает вероятность 0,26, что означает около 26% вероятности завершения работы над проектом на 60-ю единицу времени или ранее. Аналогичный способ расчетов можно использовать для любого пути или участка пути в сети.
Когда менеджер располагает подобными данными, он может принимать решения о принятии или снижении риска, связанного с продолжительностью конкретного проекта. Например, если управляющий проектом хочет увеличить возможность завершить работу над проектом за 64 единицы времени, то возможны как минимум два варианта. Первый — управленец может потратить средства на изменение условий, которые сократят длительность одной или более операций на критическом пути. Второй, более дальновидный, — выделить средства в фонд на случай непредвиденных обстоятельств и посмотреть, как будут развиваться события по мере выполнения проекта.
PERT-моделирование.
Для этой методики необходима компьютерная программа, моделирующая отпущенные на проект время, затраты и/или наличие ресурсов с использованием метода Monte Carlo Technique. Например, используя оценки времени, разработанные PERT, моделирование создает вероятность того, что любая операция или путь могут стать критическими. Для представления пределов и средней продолжительности каждой операции программа использует простое треугольное распределение Моделирование распределения продолжительности каждой операции проекта дает систему величин значений операций, которая используется для расчета критического пути. Для определения «критичности» каждой операции или пути этот процесс повторяют сотни раз. Аналогичным способом можно имитировать затраты, то есть использо-.
7—2863.
вать верхний и нижний предел оценок затрат на каждую операцию и на каждое испытание модели.
Используя программу ограниченных ресурсов с программой моделирования продолжительности PERT, можно выявить и оценить потенциальные проблемы с ресурсами. Решения по сохранению или переадресации рисков принимаются с помощью информации, полученной в результате моделирования времени, затрат и ресурсов. Существуют компьютерные программы, с помощью которых можно моделировать PERT и продолжительность PERT.
PERT и моделирование PERT применяются в проектах чрезвычайной важности, которым присуща большая степень неопределенности и где в достаточной степени точно можно рассчитать время на выполнение операций.
Вопросы для повторения.
1.
Каким образом информация по PERT отличается от информации по СРМ?.
2.
Как с помощью PERT рассчитать вероятность конкретной продолжительности выполнения проекта? Какие подходы лежат в основе этого метода?.
3.
Почему на практике метод PERT используется редко?.
Упражнения.
1. Ваша проектная команда собрала следующую информацию. Вас просят определить вероятность выполнения проекта к срокам 20 и 23, Используя метод, указанный в приложении 4-2 главы 4, начертите сеть проекта.
Операция | а | т | Ь | t. - > в | Ub-a/6f |
1—2 | 1 | 7 | 13 | _ | __ |
1—3 | 4 | 7 | 10 | - | - |
1—4 | 16 | 19 | 28 | - | - |
2—5 | 6 | 9 | 24 | - | - |
3—6 | 2 | 5 | 14 | - | - |
6—7 | 5 | 8 | 17 |
Операция | а | т | Ь | f. в | ЦЬ-а)/6У |
1—2 | 3 | 6 | 9 | _ | _ |
2—3 | 6 | 9 | 24 | - | - |
2—4 | 15 | 27 | 45 | - | - |
2—5 | 2 | 5 | 14 | - | - |
3—6 | 17 | 29 | 47 | - | - |
4—6 | 5 | 8 | 17 | - | - |
5—6 | 4 | 10 | 28 | - | - |
6—7 | 5 | 8 | 11 | — |
УЧЕБНАЯ СИТУАЦИЯ International Capital Inc — часть А.
International Capital Inc. (IC) — небольшой инвестиционный банк, обеспечивающий фонды мелким и средним фирмам. 1C использует стандартизированный формат проекта для каждого соглашения. Стандартную сеть могут изменить только либо время операций, либо необычные обстоятельства. Бет Браун была прикреплена к данному клиенту в качестве партнера управляющего проектом и разработала информационную сеть и время операций для клиента, приводимую ниже:
Операция | Описание | Непосредственно. предшествующая. операция |
В | Получите полную информацию о фирме-заказчике | — |
D | Скоординируйте с заказчиком предложения | С |
по его запросам | ||
Е | Рассчитайте будущие потребности и потоки наличности | С |
G | Подготовьте и завизируйте юридические | С |
документы | ||
Н | Объедините все черновые проекты в один | D, F, G |
1 | Учтите все возможные источники капитала | G, F |
К | Подпишите контракты и передайте фонды | и |
Время в рабочих днях
Операция. А | Оптимистичный. сценарий. 4 | Наиболее. вероятный. 7 | Пессимистичный. сценарий. 10 |
В | 2 | 4 | 8 |
С | 2 | 5 | 8 |
D | 16 | 19 | 28 |
Е | 6 | 9 | 24 |
F | 1 | 7 | 13 |
G | 4 | 10 | 28 |
Н | 2 | 5 | 14 |
1 | 5 | 8 | 17 |
J | 2 | 5 | 8 |
К | 17 | 29 | 45 |
Отчет управляющего.
Браун и другие партнеры-управляющие обычно проводят свои планы через комитет оценки проекта. Этот комитет, в котором заседают их коллеги, по традиции проверяет, учтены ли все детали, реально ли рассчитано время, есть ли в наличии все ресурсы. Браун предлагает вам разработать отчы представляющий собой запланированный график с указанием ожидаемого времени выполнения проекта в днях. В отчет включите сеть проекта Средняя продолжительность для поиска ресурсов основного проекта — 70 рабочих дней. Партнеры 1C согласились, что целесообразно работать с проектами, имеющими 95%-ную вероятность уложиться в план. Насколько данный проект соответствует среднему проекту? Каков должен быть средний показатель для обеспечения 95% вероятности выполнить проект за 70 рабочих дней?
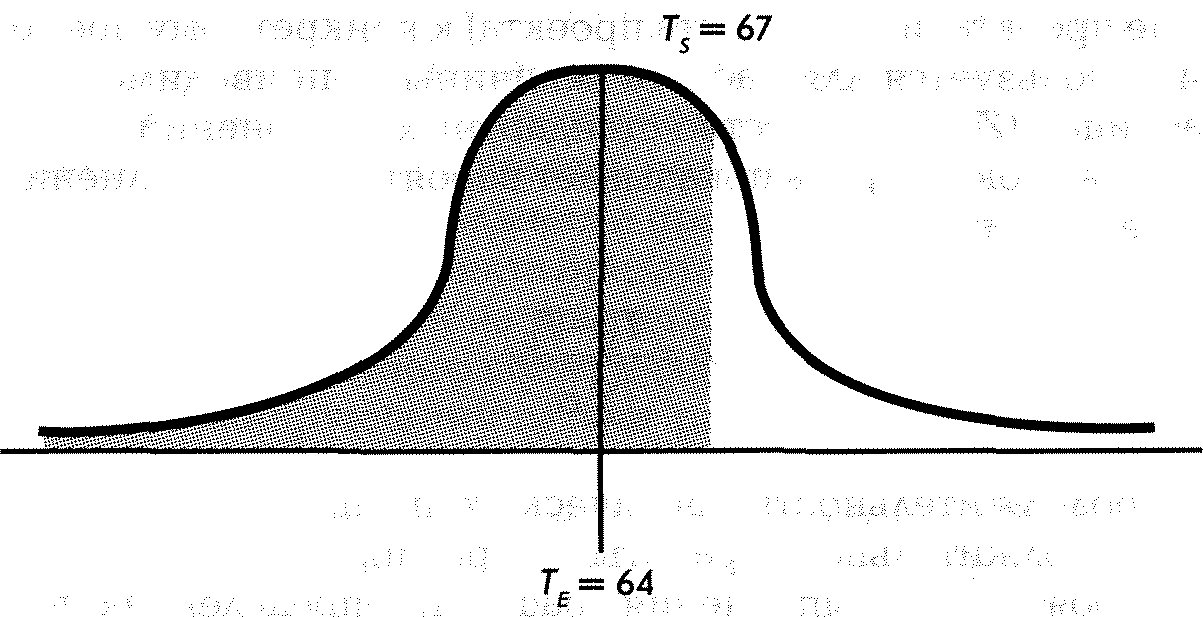
Рис. А5-3. Возможная продолжительность проекта
T
s
= 67
Используя формулу для значения Z, можно рассчитать вероятность следующим образом:
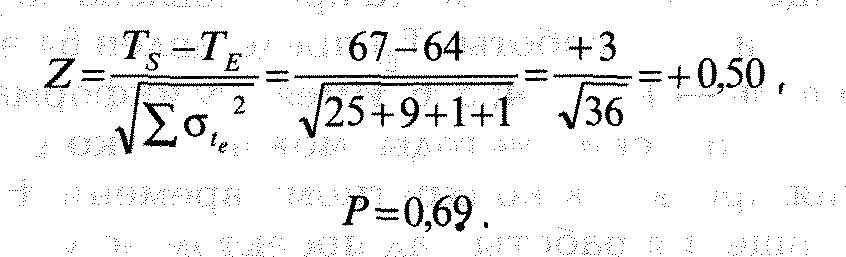
По данным таблицы А 5-2 значение Z + 0,5 дает вероятность 0,69, что означает 69%-ную вероятность завершения работы над проектом на 67-ю единицу времени или ранее.